1627. Graph Connectivity With Threshold
Description


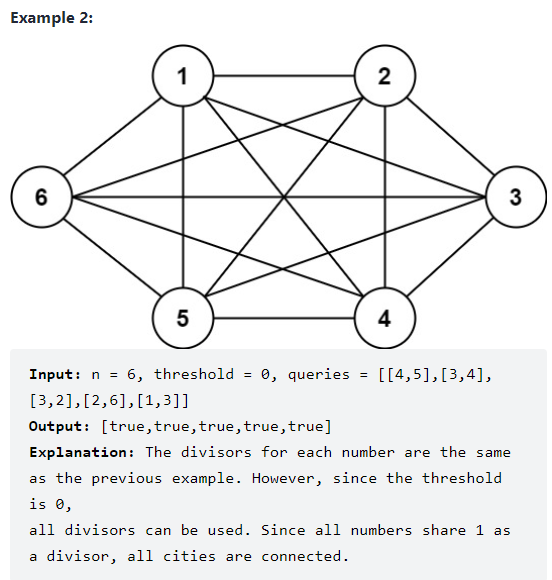

Solution
Obviously we need to use UF set.
The problem here is how to enumerate the gcd of two number. I firstly just iterate n^2 numbers pairs and try to find their common factors and got TLE.
–> We could start from the factor and to enumerate its multiples.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| class UF{
public:
vector<int> uf, size;
UF(int n):uf(n), size(n){
for(int i = 0; i < n; i++){
uf[i] = i;
size[i] = 1;
}
}
void Union(int x, int y){
int fx = find(x), fy = find(y);
if(fx == fy) return;
uf[fx] = fy;
size[fy] += size[fx];
}
int find(int x){
if(uf[x] != x){
uf[x] = find(uf[x]);
}
return uf[x];
}
int get_size(int x){
int fx = find(x);
return size[fx];
}
};
class Solution {
public:
vector<bool> areConnected(int n, int threshold, vector<vector<int>>& queries) {
vector<bool> res(queries.size(), true);
if(threshold == 0){
return res;
}
UF uf(n+1);
for(int i = threshold + 1; i < n; i++){
for(int p = i, q = 2 * i; q <= n; p += i, q += i){
uf.Union(p,q);
}
}
for(int i =0 ; i < queries.size(); i++){
res[i] = uf.find(queries[i][0]) == uf.find(queries[i][1]);
}
return res;
}
};
|







